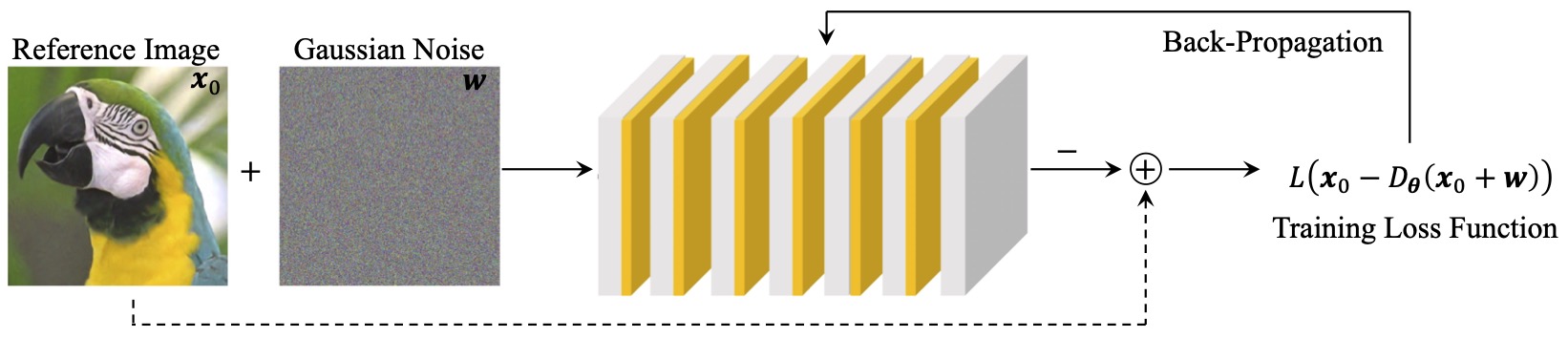
Figure 1: Image priors for PnP can be obtained by training CNNs to remove AWGN from a set of images.
Abstract
Plug-and-Play Priors (PnP) is one of the most widely-used frameworks for solving computational imaging problems through the integration of physical models and learned models. PnP leverages high-fidelity physical sensor models and powerful machine learning methods for prior modeling of data to provide state-of-the-art reconstruction algorithms. PnP algorithms alternate between minimizing a data-fidelity term to promote data consistency and imposing a learned regularizer in the form of an image denoiser. Recent highly-successful applications of PnP algorithms include bio-microscopy, computerized tomography, magnetic resonance imaging, and joint ptycho-tomography. This article presents a unified and principled review of PnP by tracing its roots, describing its major variations, summarizing main results, and discussing applications in computational imaging. We also point the way towards further developments by discussing recent results on equilibrium equations that formulate the problem associated with PnP algorithms.
Deep Model-Based Architectures

Figure 2: The PnP framework is related to two other popular computational-imaging paradigms, deep unfolding (DU) and deep equilibrium models (DEQ). A PnP algorithm, such as PnP-ISTA or RED-SD, can be turned into a DU architecture by truncating the algorithm to a fixed number of iterations and training the weights of the CNN prior end-to-end. Similarly, a DEQ architecture can be obtained by running the PnP algorithm until convergence and using the implicit differentiation at the fixed point to train the weights. The CNN operator in DU/DEQ is not necessarily an AWGN denoiser, instead it is an artifact-removal (AR) operator trained to remove artifacts specific to the PnP iterations
Applications of PnP

Figure 3: A single pre-trained CNN denoiser in PnP can address different super-resolution factors.
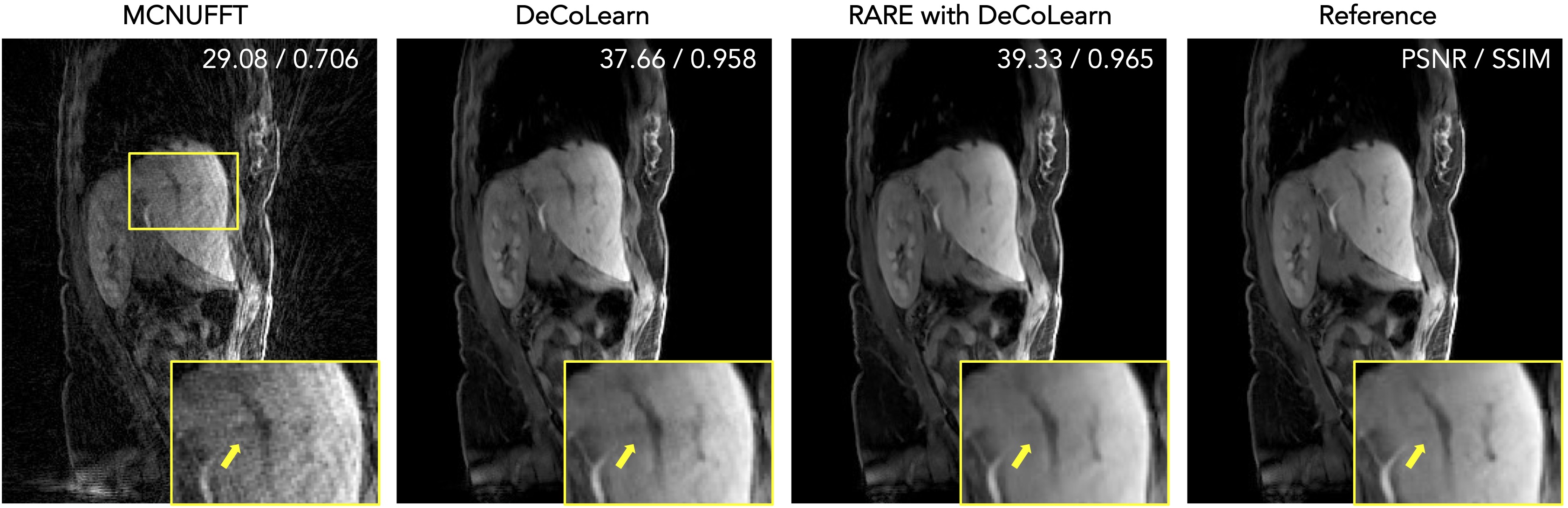
Figure 4: PnP algorithms explicitly separate the application of the forward model from that of the learned prior, enabling the adaptation of trained CNNs to new sensor configurations. This is illustrated on experimentally collected 3D MRI data corresponding to 800 radial spokes (scans of about 2 minute). MCNUFFT refers to a simple inversion of the measurement operator without any regularization. DeCoLearn is a CNN that was trained under a mismatched sensor configuration corresponding to 1600 lines (scans of about 4 minutes). A variant of PnP called RARE is used to adapt DeCoLearn to the desired 800 line data. The results of the DeCoLearn reconstruction using all the available 2000 lines is shown as Reference. The numbers on the top-right corner correspond to the relative PSNR/SSIM values with respect to Reference. Note the ability of RARE to successfully adapt DeCoLearn to 800-line data.

Figure 5: Visual evaluation of color image recovery in compressive sensing from random projections with 20% subsampling. The results of total variation (TV) and a well-known deep unfolding (DU) architecture ISTA-Net+ are provided for reference. The methods PnP (denoising) and RED (denoising) use a pre-trained AWGN denoiser as an image prior. The method PnP (AR) uses a problem-dependent artifact-removal (AR) operator pre-trained using DU. Note that the choice of denoiser affects the reconstruction significantly (PSNR shown in white).
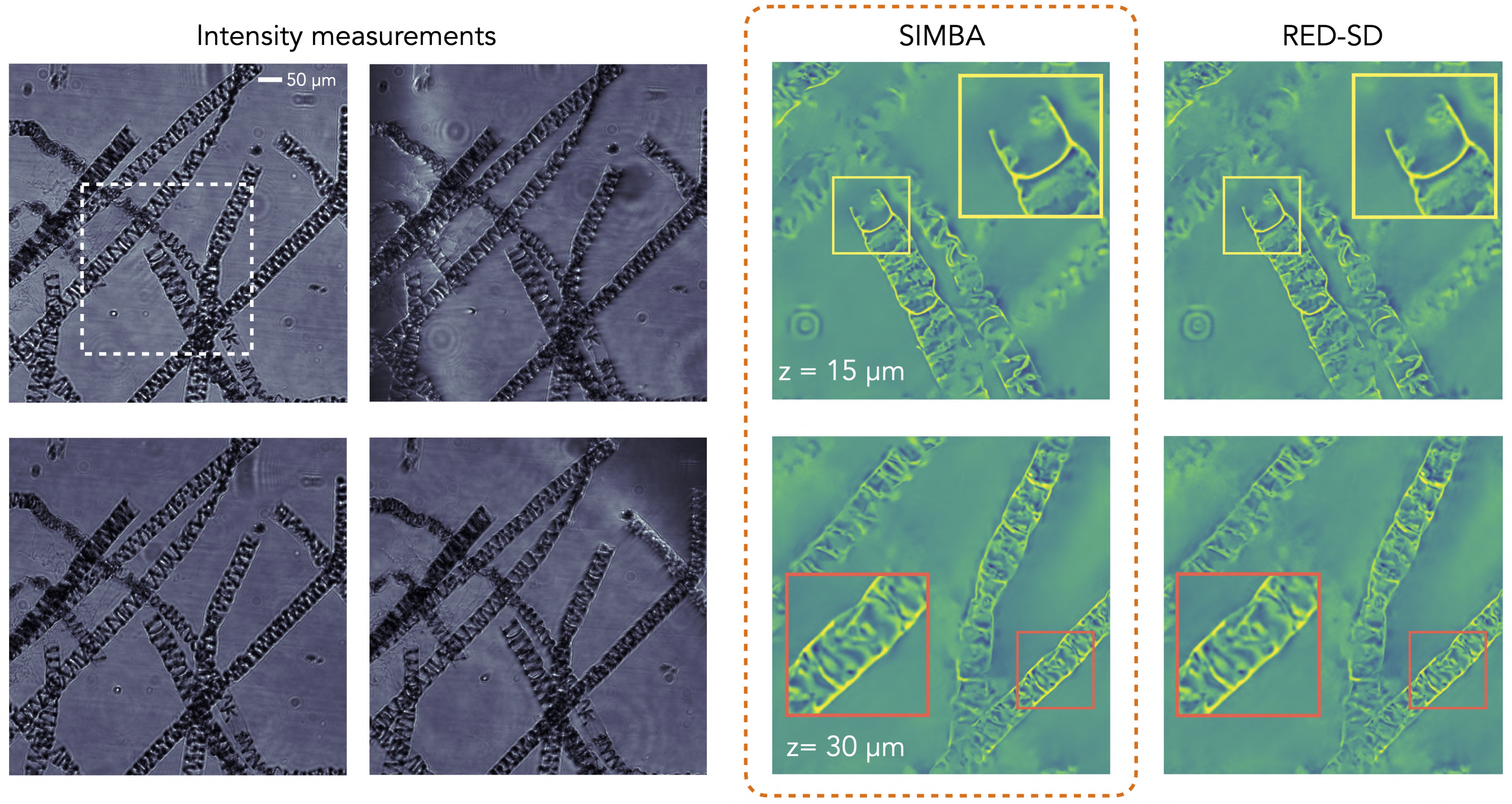
Figure 6: Online PnP algorithms, such as SIMBA, can reduce the computational and memory complexity of PnP. Here, we show the reconstruction of a 3D algae sample from 89 experimentally collected intensity diffraction tomography (IDT) measurements (see four images on the left). SIMBA, which uses minibatches of size p = 10, is compared against RED-SD, which uses all b = 89 measurements at each iteration. Both algorithms use exactly the same measurement model and the same DnCNN AWGN denoiser. Note how the results of SIMBA are indistinguishable from RED-SD even though the per-iteration complexity of SIMBA is only a fraction of that of RED-SD.
