Abstract
Deep neural networks trained as image denoisers are widely used as priors for solving imaging inverse problems. While Gaussian denoising is thought sufficient for learning image priors, we show that priors from deep models pre-trained as more general restoration operators can perform better. We introduce Stochastic deep Restoration Priors (ShaRP), a novel method that leverages an ensemble of such restoration models to regularize inverse problems. ShaRP improves upon methods using Gaussian denoiser priors by better handling structured artifacts and enabling self-supervised training even without fully sampled data. We prove ShaRP minimizes an objective function involving a regularizer derived from the score functions of minimum mean square error (MMSE) restoration operators, and theoretically analyze its convergence. Empirically, ShaRP achieves state-of-the-art performance on tasks such as magnetic resonance imaging reconstruction and single-image super-resolution, surpassing both denoiser- and diffusion-model-based methods without requiring retraining.
Stochastic Deep Restoration Priors (ShaRP)

Figure 1: ShaRP solves imaging inverse problems by using a restoration network trained on a set of tasks as an image prior.
ShaRP for Acclerated MRI
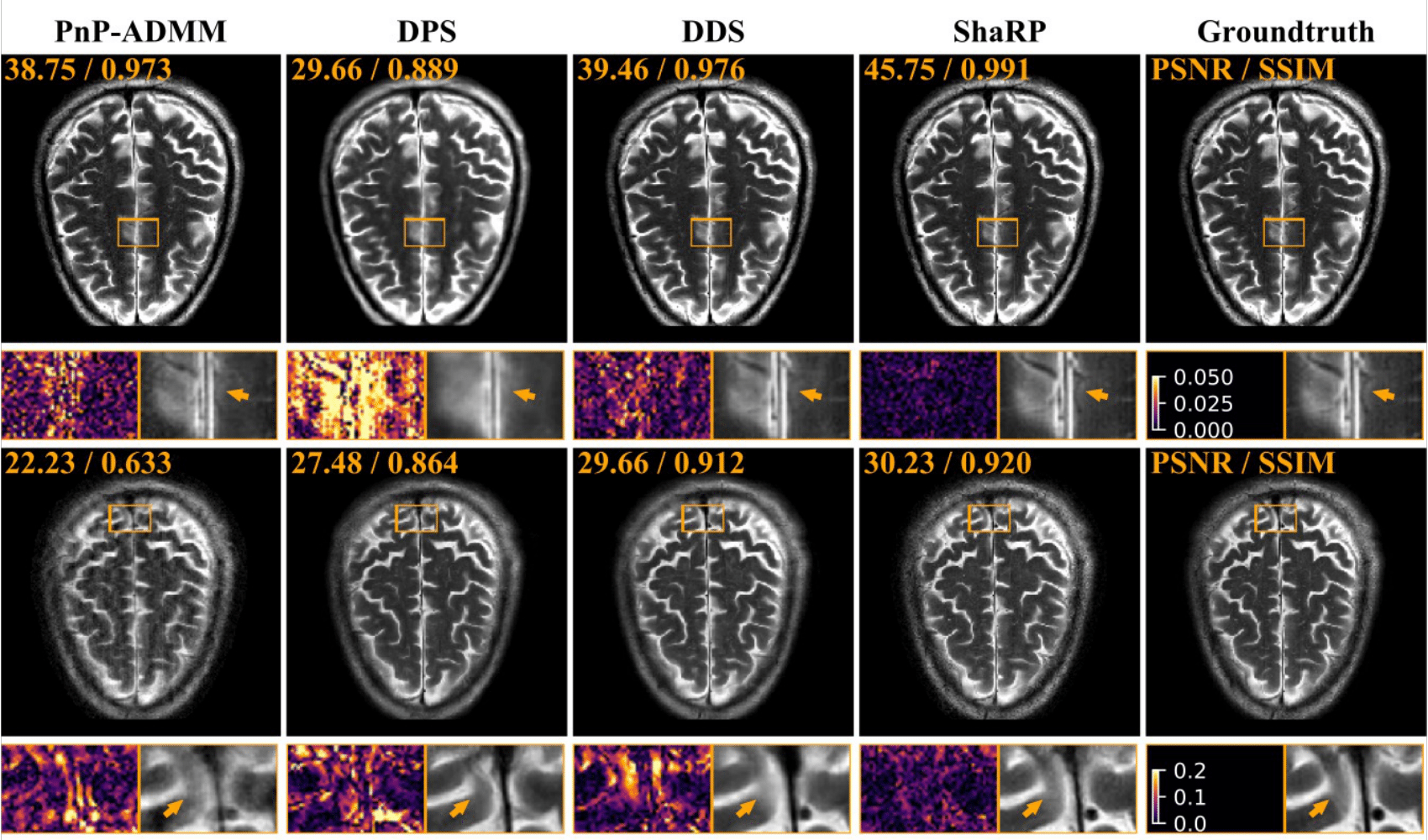
Figure 1: Visual comparison of ShaRP with baseline methods on CS-MRI. Error maps and zoomed-in areas highlight differences. Note how ShaRP with stochastic priors outperforms state-of-the-art methods using denoiser and diffusion-model priors.
ShaRP for Single Image Super Resolution

Figure 2: Visual comparison of ShaRP with several well-known methods on SISR. Note how ShaRP successfully recovers most features and maintains high data consistency with the available measurements.
Convergence Behaviour of ShaRP
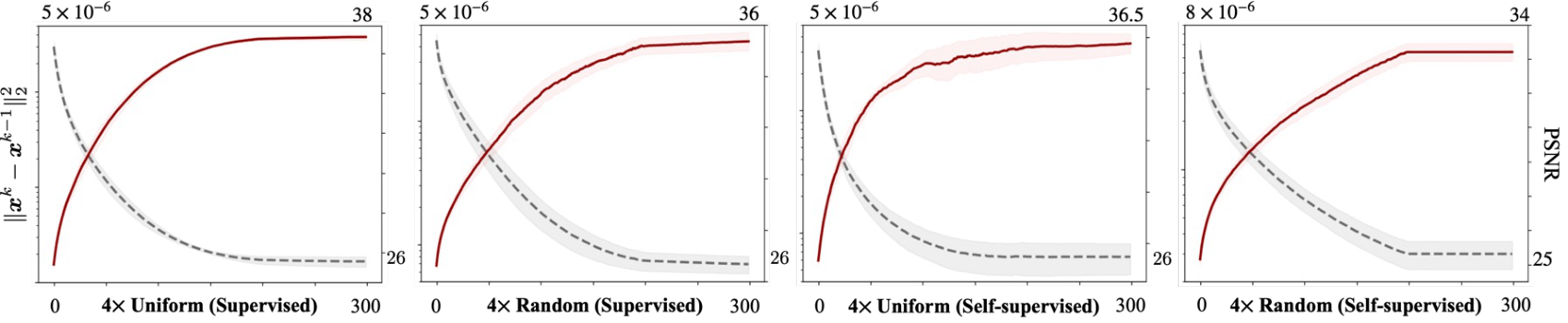
Figure 3: Convergence of ShaRP for 4 times accelerated MRI reconstruction on the fastMRI dataset. (a)-(b) depict the convergence behavior of ShaRP using restoration operators trained in a supervised manner, while (c)-(d) correspond to those trained in a self-supervised manner.
Illustration of the benefit of using a ensemble of restoration priors

Figure 4: Illustration of the impact of using an ensemble of restoration priors. ShaRP (ensemble of priors) consistently outperforms DRP (fixed prior) by recovering finer details, leading to higher PSNR and SSIM scores, along with improved perceptual quality.