Abstract
Posterior sampling has been shown to be a powerful Bayesian approach for solving imaging inverse problems. The recent plug-and-play unadjusted Langevin algorithm (PnP-ULA) has emerged as a promising method for Monte Carlo sampling and minimum mean squared error (MMSE) estimation by combining physical measurement models with deep-learning priors specified using image denoisers. However, the intricate relationship between the sampling distribution of PnP-ULA and the mismatched data-fidelity and denoiser has not been theoretically analyzed. We address this gap by proposing a posterior-L2 pseudometric and using it to quantify an explicit error bound for PnP-ULA under mismatched posterior distribution. We numerically validate our theory on several inverse problems such as sampling from Gaussian mixture models and image deblurring. Our results suggest that the sensitivity of the sampling distribution of PnP-ULA to a mismatch in the measurement model and the denoiser can be precisely characterized.
Numerical Experiments
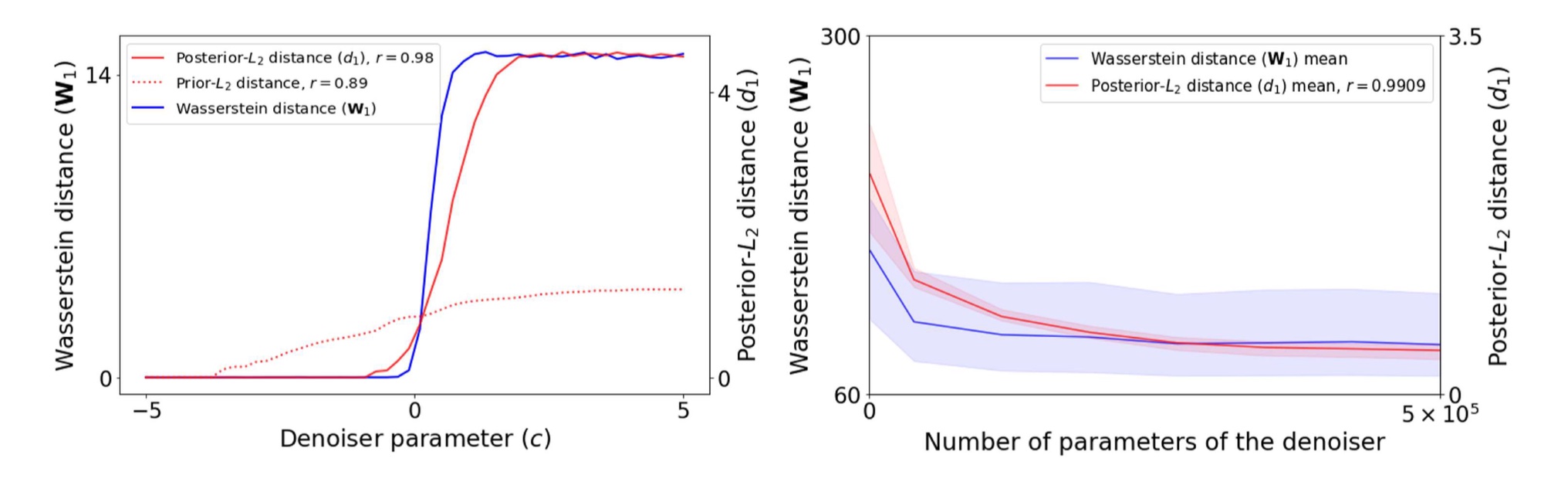
Figure 1: Illustration of Theorem 1's bound by visualizing the strong correlation between the Wasserstein distance between sampling distributions and the posterior-L2 distance between denois- ers. Left plot: Distances, for the GMM experiment in 2D, computed between sampling generated by mismatch denoisers and the exact MMSE denoiser. Note how the posterior-L2 is more correlated to the Wasserstein distance than the prior-L2. Right plot: Distances, for the gray-scale images experi- ment, compute between DnCNN denoisers with 5 × 105 weights and other DnCNN denoisers with fewer weights. Note how the posterior-L2 and the Wasserstein distance are highly correlated with correlation r = 0.9909 in average and r > 0.97 for each image.
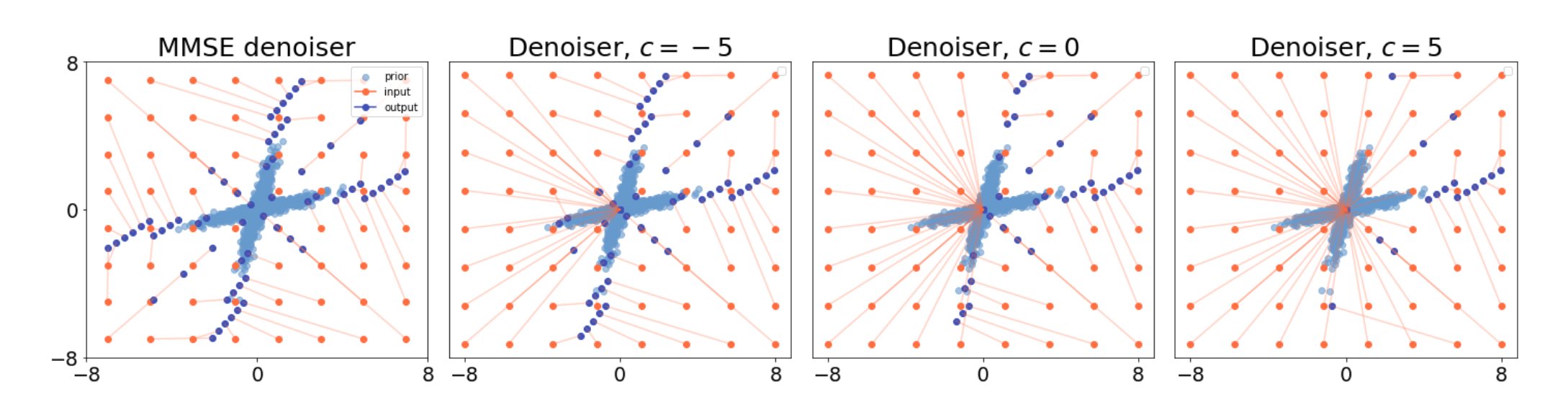
Figure 2: Illustration of denoisers with ε = 0.05 used for the 2D Gaussian Mixture experiment. The prior distribution, a Gaussian Mixture, is represented in light blue. Denoisers, Dε : R2 → R2, are represented by there outputs (in dark blue) on a set of inputs (in orange) linked together (by orange lines). Rightmost: Exact MMSE denoiser. Leftmost: Three mismatched denoisers with various c parameters.

Figure 3: Illustration of MMSE estimators computed by PnP-ULA run on 105 steps with various DnCNN denoisers. The quantities in the top-left corner of each image provide PSNR and SSIM values for each reconstructed images. Denoisers have a different number of weights, but are all trained in the same way. Note that a shift between the reference denoiser (5 × 105 weights) and mismatched denoisers using less weights (103 or 105 weights) implies a shift in the MMSE estimator quality.

Figure 4: Illustration of the PnP-ULA stability to a mismatch forward model. Leftmost six plots: MMSE estimators computed with PnP-ULA run on 30,000 steps on Gaussian blur. Rightmost: Evolution of the Wasserstein distance between sampling distributions computed with a mismatched blur kernels and sampling with the exact forward model. Note that the image reconstruction quality improves as blur approaches the one used to degrade the image. In addition, in the case of Gaussian blur, the pseudometric justifies qualitatively the observed linear decrease of the Wasserstein distance.
