
Illustration of using the traditional deep equilibrium model (DEQ) and the proposed framework. While the regularization in the traditional DEQ approach is implicit in the CNN, our method learns an explicit regularization functional that minimizes a mean-squared error metric. Note how learning an explicit regularizer does not compromise the PSNR performance relative to DEQ.
Abstract
There has been significant recent interest in the use of deep learning for regularizing imaging inverse problems. Most work in the area has focused on regularization imposed implicitly by convolutional neural networks (CNNs) pre-trained for image reconstruction. In this work, we follow an alternative line of work based on learning explicit regularization functionals that promote preferred solutions. We develop the Explicit Learned Deep Equilibrium Regularizer (ELDER) method for learning explicit regularizers that minimize a mean-squared error (MSE) metric. ELDER is based on a regularization functional parameterized by a CNN and a deep equilibrium learning (DEQ) method for training the functional to be MSE-optimal at the fixed points of the reconstruction algorithm. The explicit regularizer enables ELDER to directly inherit fundamental convergence results from optimization theory. On the other hand, DEQ training enables ELDER to improve over existing explicit regularizers without prohibitive memory complexity during training. We use ELDER to train several approaches to parameterizing explicit regularizers and test their performance on three distinct imaging inverse problems. Our results show that ELDER can greatly improve the quality of explicit regularizers compared to existing methods, and show that learning explicit regularizers does not compromise performance relative to methods based on implicit regularization.
Improvement over Regularizers based on Image Denoising

Figure 1: Comparison between ELDER and GSPnP for single image super-resoluion. Both methods seek to learn explicit regularizers parametrized by the same CNN architecture, but are trained differently. Left: Evolution of the PSNR is plotted against iteration number for both methods. Right: Visual illustration of iterates obtained by GSPnP (top) and ELDER (bottom). Note how ELDER outperforms GSPnP due to its ability to learn regularizers that minimize MSE.
Applications of ELDER

Figure 2: Visual comparison of ELDER against several well-known methods on the problem of single image super-resolution (SISR) with scale d = 3 (top) and d = 4 (bottom). The blur kernels are shown in the zoomed low-resolution (LR) images, respectively. Note how ELDER significantly improves over GSPnP, a recent method for learning explicit regularizers. Additionally, it performs better than DEQ and DPIR, both of which rely on implicit regularization specified by a CNN. This figure shows that ELDER learns explicit regularizers without compromising image quality.

Figure 3: Comparison of ELDER relative to DPIR, GSPnP and DEQ for image inpainting with masked probability of p = 0.7 on CBSD68. Note that ELDER provides substantial improvements over PnP image reconstruction methods, matching the performance of DEQ.

Figure 4: Evaluation of several well-known methods on reconstruction of a brain image from its radial Fourier measurements at 10% sampling. Note how ELDER outperforms DPIR, GSPnP, and the traditional DEQ both quantitatively and visually.
Explicit Parametrization Strategies
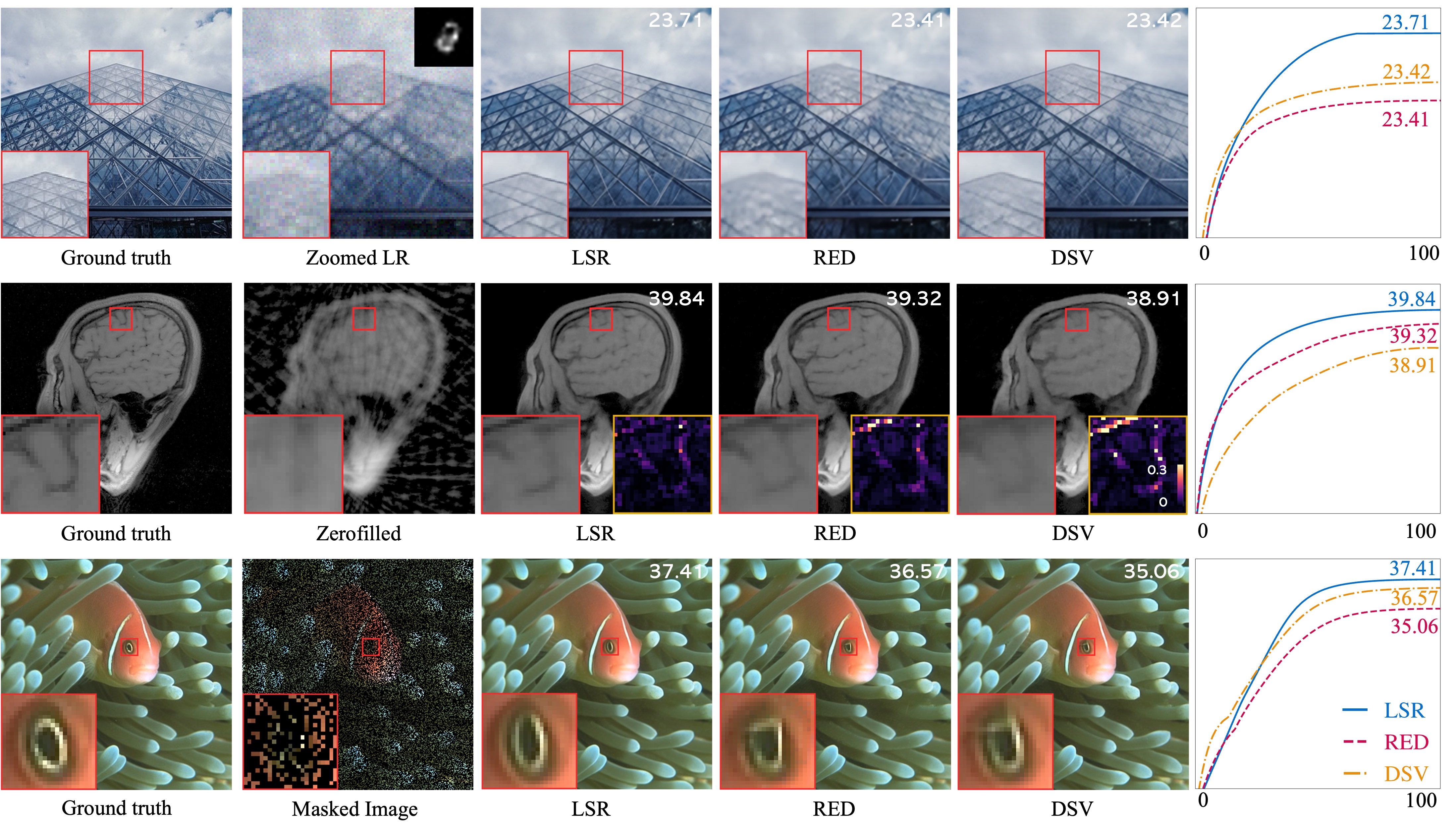
Figure 5: Visual illustration of the results obtained by ELDER using the three parameterization approaches for the regularization functional. We show results for three inverse problems: image super-resolution (top), reconstruction from Fourier samples (middle), and image inpainting (bottom). The rightmost panel plots the evolution of PSNR (dB) accross forward iterations. Note how LSR achieves an overall better performance compared to DSV and RED.
