Figure 1: Illustration of slices from a luggage reconstructed using Filtered Back Projection (FBP), Diffusion Posterior Sampling (DPS), and the proposed DOLCE method. Note the remarkable accuracy of the DOLCE reconstructions that preserve fine details.
Abstract
Limited-Angle Computed Tomography (LACT) is a non-destructive 3D imaging technique used in a variety of applications ranging from security to medicine. The limited angle coverage in LACT is often a dominant source of severe artifacts in the reconstructed images, making it a challenging imaging inverse problem. Diffusion models are a recent class of deep generative models for synthesizing realistic images using image denoisers. In this work, we present Diffusion Probabilistic Limited-Angle CT Reconstruction (DOLCE) as the first framework for integrating conditionally-trained diffusion models and explicit physical measurement models for solving imaging inverse problems. DOLCE achieves the SOTA performance in highly ill-posed LACT by alternating between the data-fidelity and sampling updates of a diffusion model conditioned on the transformed sinogram. We show through extensive experimentation that unlike existing methods, DOLCE can synthesize high-quality and structurally coherent 3D volumes by using only 2D conditionally pre-trained diffusion models. We further show on several challenging real LACT datasets that the same pre-trained DOLCE model achieves the SOTA performance on drastically different types of images.
DOLCE for 3D LACT Reconsturction (90º view)

Figure 2: 3D rendering of a luggage (Row 1) from its 2D slices (Row 2) reconstructed using FBP, DPS, and DOLCE from the limited-angle CT data containing just one-third of the views from angle range 0-60◦.
Medical CT
Security Check-in CT
Figure 3: Evolution of the synthesized 3D images accross DOLCE iterates. Left image shows a medical CT image, while the right image shows a luggage CT.
Comparison of Reconstruction Performance on Two Dataset
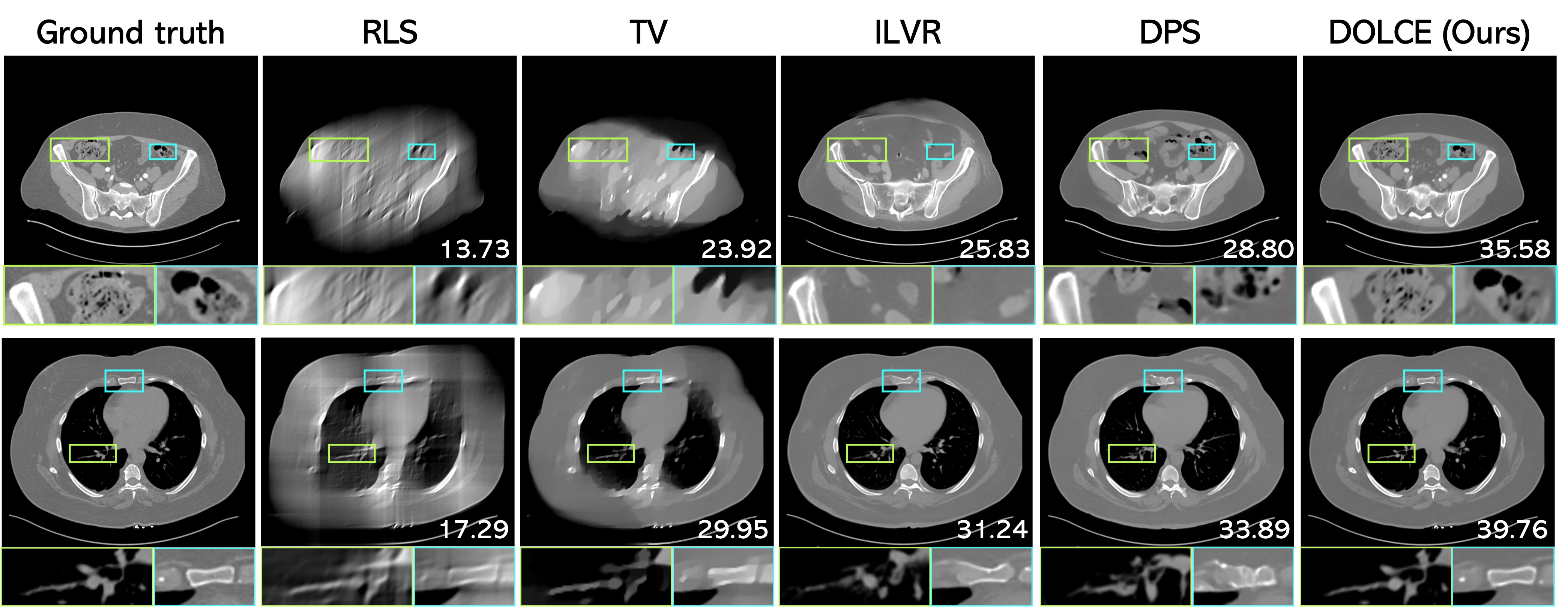
Figure 4: Visual evaluation of limited angle tomographic reconstruction in body CT scan, where the input measurements are captured respectively from an angular coverage of 60º (top) and 90º (bottom), respectively. PSNR (dB) is indicated at bottom for each reconstruction, measured against the ground truth.
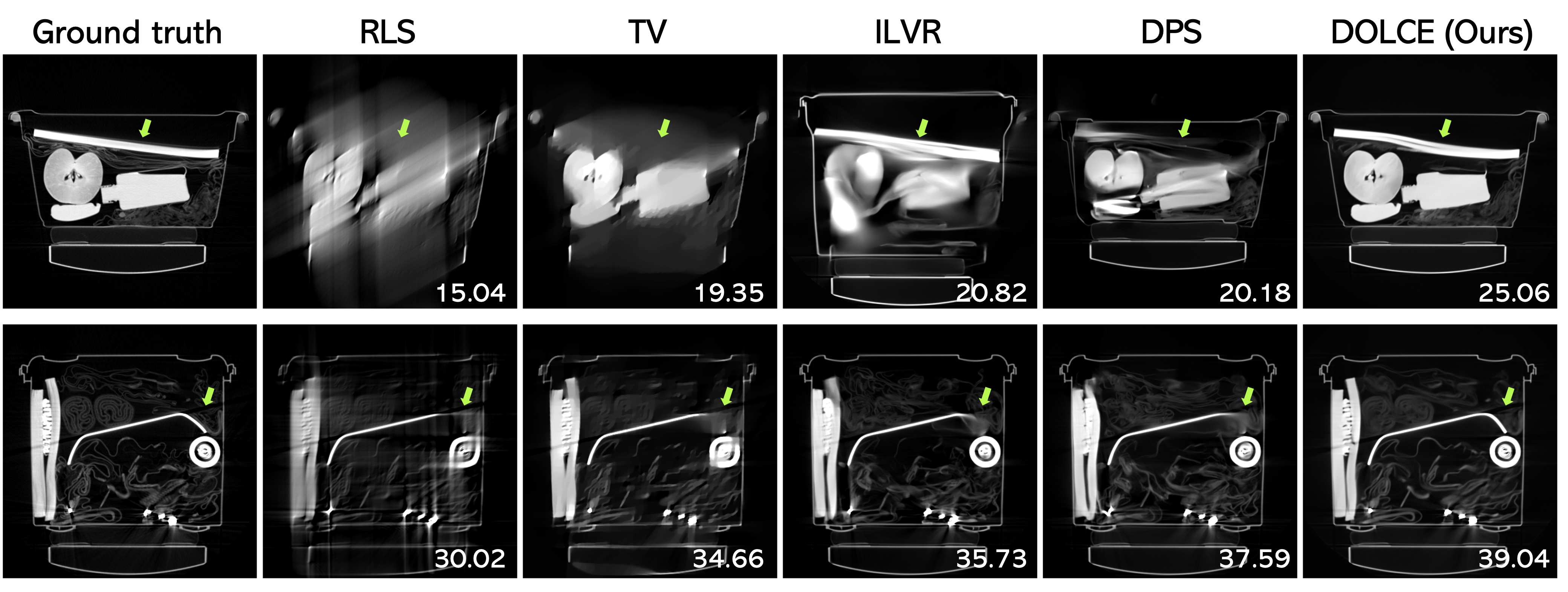
Figure 5: Visual evaluation of limited angle tomographic reconstruction in security check-in luggage CT scan, where the input measurements are captured respectively from an angular coverage of 60º (top) and 90º (bottom), respectively.
Additional Ablation Studies
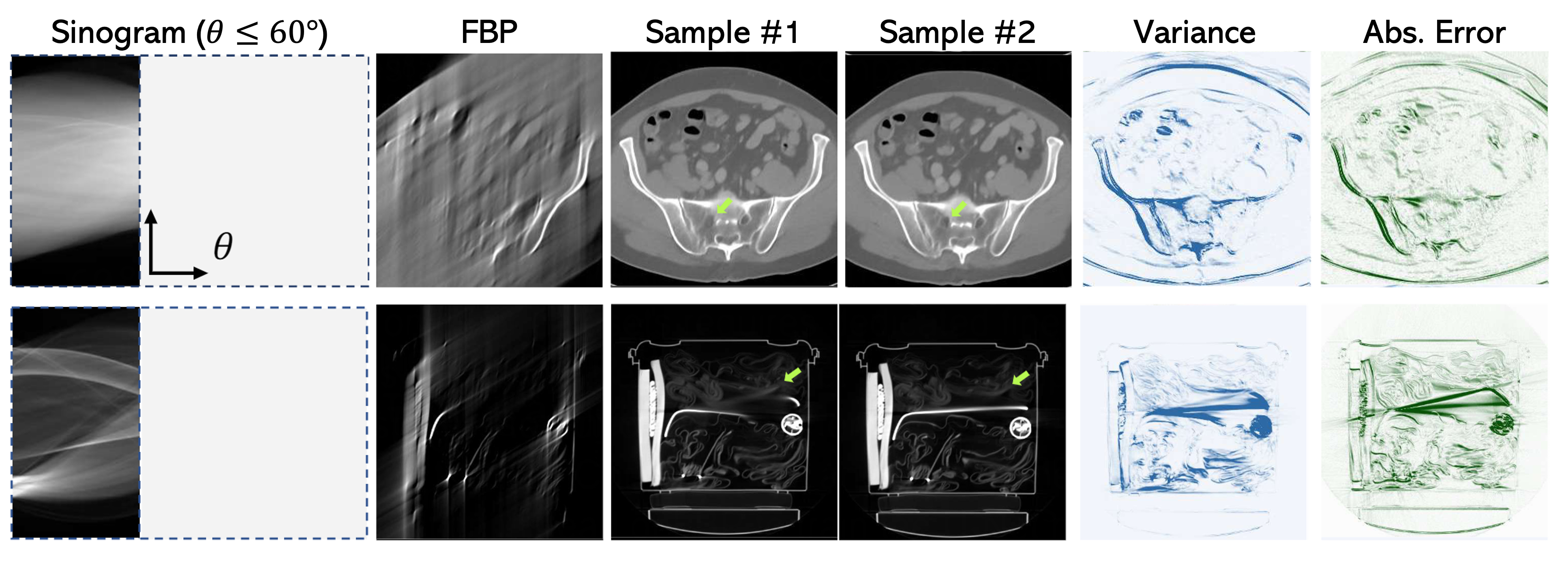
Figure 6: Visual results on two different CT images. The error to the ground truth is computed using the conditional mean and the variance corresponds to per-pixel standard deviation. It is evident that the ill-posed nature of the reconstruction task has a direct impact on the diversity of the generated samples, and the variances are highly correlated with the reconstruction errors.

Figure 7: We use a region growing 3D segmentation in all cases and the resulting segmentations are highlighted in color, against a 3D rendering of the reconstructed 2D slices using half of view. Note that our method performs very similar to ground truth in determining the object boundaries compared to RLS and DPS.
